UNDERSTANDING OPTION GREEKS
Use of the Greeks[edit]
| ||||||||||||||||||||||||||||||||||||||
|
The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging.
The Greeks in the Black–Scholes modelare relatively easy to calculate, a desirable property of financial models, and are very useful for derivatives traders, especially those who seek to hedge their portfolios from adverse changes in market conditions. For this reason, those Greeks which are particularly useful for hedging--such as delta, theta, and vega--are well-defined for measuring changes in Price, Time and Volatility. Although rho is a primary input into the Black–Scholes model, the overall impact on the value of an option corresponding to changes in the risk-free interest rate is generally insignificant and therefore higher-order derivatives involving the risk-free interest rate are not common.
The most common of the Greeks are the first order derivatives: Delta, Vega, Theta and Rhoas well as Gamma, a second-order derivative of the value function. The remaining sensitivities in this list are common enough that they have common names, but this list is by no means exhaustive.
First-order Greeks[edit]
Delta[edit]
 |
Delta,[4]  , measures the rate of change of the theoretical option value with respect to changes in the underlying asset's price. Delta is the first derivative of the value
, measures the rate of change of the theoretical option value with respect to changes in the underlying asset's price. Delta is the first derivative of the value 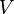 of the option with respect to the underlying instrument's price
of the option with respect to the underlying instrument's price  .
.
 , measures the rate of change of the theoretical option value with respect to changes in the underlying asset's price. Delta is the first derivative of the value
, measures the rate of change of the theoretical option value with respect to changes in the underlying asset's price. Delta is the first derivative of the value 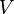 of the option with respect to the underlying instrument's price
of the option with respect to the underlying instrument's price  .
.Practical use[edit]
For a vanilla option, delta will be a number between 0.0 and 1.0 for a long call (or a short put) and 0.0 and −1.0 for a long put (or a short call); depending on price, a call option behaves as if one owns 1 share of the underlying stock (if deep in the money), or owns nothing (if far out of the money), or something in between, and conversely for a put option. The difference of the delta of a call and the delta of a put at the same strike is close to but not in general equal to one, but instead is equal to the inverse of the discount factor. By put–call parity, long a call and short a put equals a forward F, which is linear in the spot S, with factor the inverse of the discount factor, so the derivative dF/dS is this factor.
These numbers are commonly presented as a percentage of the total number of shares represented by the option contract(s). This is convenient because the option will (instantaneously) behave like the number of shares indicated by the delta. For example, if a portfolio of 100 American call options on XYZ each have a delta of 0.25 (=25%), it will gain or lose value just like 25 shares of XYZ as the price changes for small price movements. The sign and percentage are often dropped – the sign is implicit in the option type (negative for put, positive for call) and the percentage is understood. The most commonly quoted are 25 delta put, 50 delta put/50 delta call, and 25 delta call. 50 Delta put and 50 Delta call are not quite identical, due to spot and forward differing by the discount factor, but they are often conflated.
Delta is always positive for long calls and negative for long puts (unless they are zero). The total delta of a complex portfolio of positions on the same underlying asset can be calculated by simply taking the sum of the deltas for each individual position – delta of a portfolio is linear in the constituents. Since the delta of underlying asset is always 1.0, the trader coulddelta-hedge his entire position in the underlying by buying or shorting the number of shares indicated by the total delta. For example, if the delta of a portfolio of options in XYZ (expressed as shares of the underlying) is +2.75, the trader would be able to delta-hedge the portfolio by selling short 2.75 shares of the underlying. This portfolio will then retain its total value regardless of which direction the price of XYZ moves. (Albeit for only small movements of the underlying, a short amount of time and not-withstanding changes in other market conditions such as volatility and the rate of return for a risk-free investment).
As a proxy for probability[edit]
Main article: Moneyness
The (absolute value of) Delta is close to, but not identical with, the percent moneyness of an option, i.e., the implied probability that the option will expire in-the-money (if the market moves under Brownian motion in the risk-neutral measure).[5] For this reason some option traders use the absolute value of delta as an approximation for percent moneyness. For example, if an out-of-the-money call option has a delta of 0.15, the trader might estimate that the option has approximately a 15% chance of expiring in-the-money. Similarly, if a put contract has a delta of −0.25, the trader might expect the option to have a 25% probability of expiring in-the-money. At-the-money puts and calls have a delta of approximately 0.5 and −0.5 respectively with a slight bias towards higher deltas for ATM calls,[note 1] i.e. both have approximately a 50% chance of expiring in-the-money. The correct, exact calculation for the probability of an option finishing at a particular price of K is its Dual Delta, which is the first derivative of option price with respect to strike.[citation needed]
Relationship between call and put delta[edit]
Given a European call and put option for the same underlying, strike price and time to maturity, and with no dividend yield, the sum of the absolute values of the delta of each option will be 1.00 – more precisely, the delta of the call (positive) minus the delta of the put (negative) equals 1. This is due to put–call parity: a long call plus a short put (a call minus a put) replicates a forward, which has delta equal to 1.
If the value of delta for an option is known, one can compute the value of the delta of the option of the same strike price, underlying and maturity but opposite right by subtracting 1 from a known call delta or adding 1 to a known put delta.
d(call) − d(put) = 1, therefore: d(call) = d(put) + 1 and d(put) = d(call) − 1.
For example, if the delta of a call is 0.42 then one can compute the delta of the corresponding put at the same strike price by 0.42 − 1 = −0.58. To derive the delta of a call from a put, one can similarly take −0.58 and add 1 to get 0.42.
Vega[edit]
 |
Vega[4] measures sensitivity to volatility. Vega is the derivative of the option value with respect to the volatility of the underlying asset.
Vega is not the name of any Greek letter. However, the glyph used is the Greek letter nu ( ). Presumably the name vega was adopted because the Greek letter nu looked like a Latin vee, and vega was derived from vee by analogy with how beta, eta, and theta are pronounced in American English. Another possibility is that it is named after Joseph De La Vega, famous forConfusion of Confusions, a book about stock markets and which discusses trading operations that were complex, involving both options and forward trades.[6]
). Presumably the name vega was adopted because the Greek letter nu looked like a Latin vee, and vega was derived from vee by analogy with how beta, eta, and theta are pronounced in American English. Another possibility is that it is named after Joseph De La Vega, famous forConfusion of Confusions, a book about stock markets and which discusses trading operations that were complex, involving both options and forward trades.[6]
 ). Presumably the name vega was adopted because the Greek letter nu looked like a Latin vee, and vega was derived from vee by analogy with how beta, eta, and theta are pronounced in American English. Another possibility is that it is named after Joseph De La Vega, famous forConfusion of Confusions, a book about stock markets and which discusses trading operations that were complex, involving both options and forward trades.[6]
). Presumably the name vega was adopted because the Greek letter nu looked like a Latin vee, and vega was derived from vee by analogy with how beta, eta, and theta are pronounced in American English. Another possibility is that it is named after Joseph De La Vega, famous forConfusion of Confusions, a book about stock markets and which discusses trading operations that were complex, involving both options and forward trades.[6]
The symbol kappa, 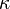 , is sometimes used (by academics) instead of vega (as is tau (
, is sometimes used (by academics) instead of vega (as is tau ( ) or capital Lambda (
) or capital Lambda (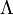 ),[7]:315 though these are rare).
),[7]:315 though these are rare).
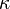 , is sometimes used (by academics) instead of vega (as is tau (
, is sometimes used (by academics) instead of vega (as is tau ( ) or capital Lambda (
) or capital Lambda (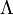 ),[7]:315 though these are rare).
),[7]:315 though these are rare).
Vega is typically expressed as the amount of money per underlying share that the option's value will gain or lose as volatility rises or falls by 1%.
Vega can be an important Greek to monitor for an option trader, especially in volatile markets, since the value of some option strategies can be particularly sensitive to changes in volatility. The value of an option straddle, for example, is extremely dependent on changes to volatility.
Theta[edit]
 |
Theta,[4]  , measures the sensitivity of the value of the derivative to the passage of time (see Option time value): the "time decay."
, measures the sensitivity of the value of the derivative to the passage of time (see Option time value): the "time decay."
 , measures the sensitivity of the value of the derivative to the passage of time (see Option time value): the "time decay."
, measures the sensitivity of the value of the derivative to the passage of time (see Option time value): the "time decay."
The mathematical result of the formula for theta (see below) is expressed in value per year. By convention, it is usual to divide the result by the number of days in a year, to arrive at the amount of money per share of the underlying that the option loses in one day. Theta is almost always negative for long calls and puts and positive for short (or written) calls and puts. An exception is a deep in-the-money European put. The total theta for a portfolio of options can be determined by summing the thetas for each individual position.
The value of an option can be analysed into two parts: the intrinsic value and the time value. The intrinsic value is the amount of money you would gain if you exercised the option immediately, so a call with strike $50 on a stock with price $60 would have intrinsic value of $10, whereas the corresponding put would have zero intrinsic value. The time value is the value of having the option of waiting longer before deciding to exercise. Even a deeply out of the money put will be worth something, as there is some chance the stock price will fall below the strike before the expiry date. However, as time approaches maturity, there is less chance of this happening, so the time value of an option is decreasing with time. Thus if you are long an option you are short theta: your portfolio will lose value with the passage of time (all other factors held constant).
Rho[edit]
 |
Rho,[4]  , measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term).
, measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term).
 , measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term).
, measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term).
Except under extreme circumstances, the value of an option is less sensitive to changes in the risk free interest rate than to changes in other parameters. For this reason, rho is the least used of the first-order Greeks.
Rho is typically expressed as the amount of money, per share of the underlying, that the value of the option will gain or lose as the risk free interest rate rises or falls by 1.0% per annum (100 basis points).
Lambda[edit]
 |
Lambda,  , omega,
, omega,  , or elasticity[4] is the percentage change in option value per percentage change in the underlying price, a measure ofleverage, sometimes called gearing.
, or elasticity[4] is the percentage change in option value per percentage change in the underlying price, a measure ofleverage, sometimes called gearing.
 , omega,
, omega,  , or elasticity[4] is the percentage change in option value per percentage change in the underlying price, a measure ofleverage, sometimes called gearing.
, or elasticity[4] is the percentage change in option value per percentage change in the underlying price, a measure ofleverage, sometimes called gearing.Second-order Greeks[edit]
Gamma[edit]
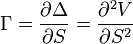 |
Gamma,[4]  , measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative of the value function with respect to the underlying price. All long options have positive gamma and all short options have negative gamma. Long options have a positive relationship with Gamma because as price increases, Gamma increases up as well, causing Delta to approach 1 from 0 (long call option) and 0 from -1 (long put option). The inverse is true for short options.[8]
, measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative of the value function with respect to the underlying price. All long options have positive gamma and all short options have negative gamma. Long options have a positive relationship with Gamma because as price increases, Gamma increases up as well, causing Delta to approach 1 from 0 (long call option) and 0 from -1 (long put option). The inverse is true for short options.[8]
 , measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative of the value function with respect to the underlying price. All long options have positive gamma and all short options have negative gamma. Long options have a positive relationship with Gamma because as price increases, Gamma increases up as well, causing Delta to approach 1 from 0 (long call option) and 0 from -1 (long put option). The inverse is true for short options.[8]
, measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative of the value function with respect to the underlying price. All long options have positive gamma and all short options have negative gamma. Long options have a positive relationship with Gamma because as price increases, Gamma increases up as well, causing Delta to approach 1 from 0 (long call option) and 0 from -1 (long put option). The inverse is true for short options.[8]
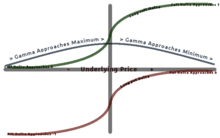
Gamma is greatest approximately at-the-money (ATM) and diminishes the further out you go either in-the-money (ITM) or out-of-the-money (OTM). Gamma is important because it corrects for the convexity of value.
When a trader seeks to establish an effective delta-hedge for a portfolio, the trader may also seek to neutralize the portfolio's gamma, as this will ensure that the hedge will be effective over a wider range of underlying price movements. However, in neutralizing the gamma of a portfolio, alpha (the return in excess of the risk-free rate) is reduced
REFERENCE:http://en.wikipedia.org/wiki/Greeks_%28finance%29
 )
)
No comments:
Post a Comment